Samodzielne obliczanie zysku z lokaty w Excelu to nie tylko umiejętność, ale prawdziwy klucz do pełnej kontroli nad własnymi finansami. W tym artykule pokażę Ci, jak krok po kroku zbudować własny, niezawodny kalkulator, który pozwoli Ci precyzyjnie oszacować realny zysk z każdej lokaty bankowej, uwzględniając wszystkie kluczowe czynniki, takie jak podatek Belki czy częstotliwość kapitalizacji odsetek.
Samodzielne obliczanie zysku z lokaty w Excelu klucz do pełnej kontroli nad finansami.
- Podatek Belki (19% od zysków) jest kluczowy do poznania realnego zysku netto i zawsze należy go uwzględnić w obliczeniach.
- Częstotliwość kapitalizacji odsetek (roczna, miesięczna, dzienna) ma znaczący wpływ na ostateczny zysk i musi być poprawnie uwzględniona w formule.
- Dla lokat krótszych niż rok, oprocentowanie roczne należy proporcjonalnie dostosować do faktycznego czasu trwania inwestycji.
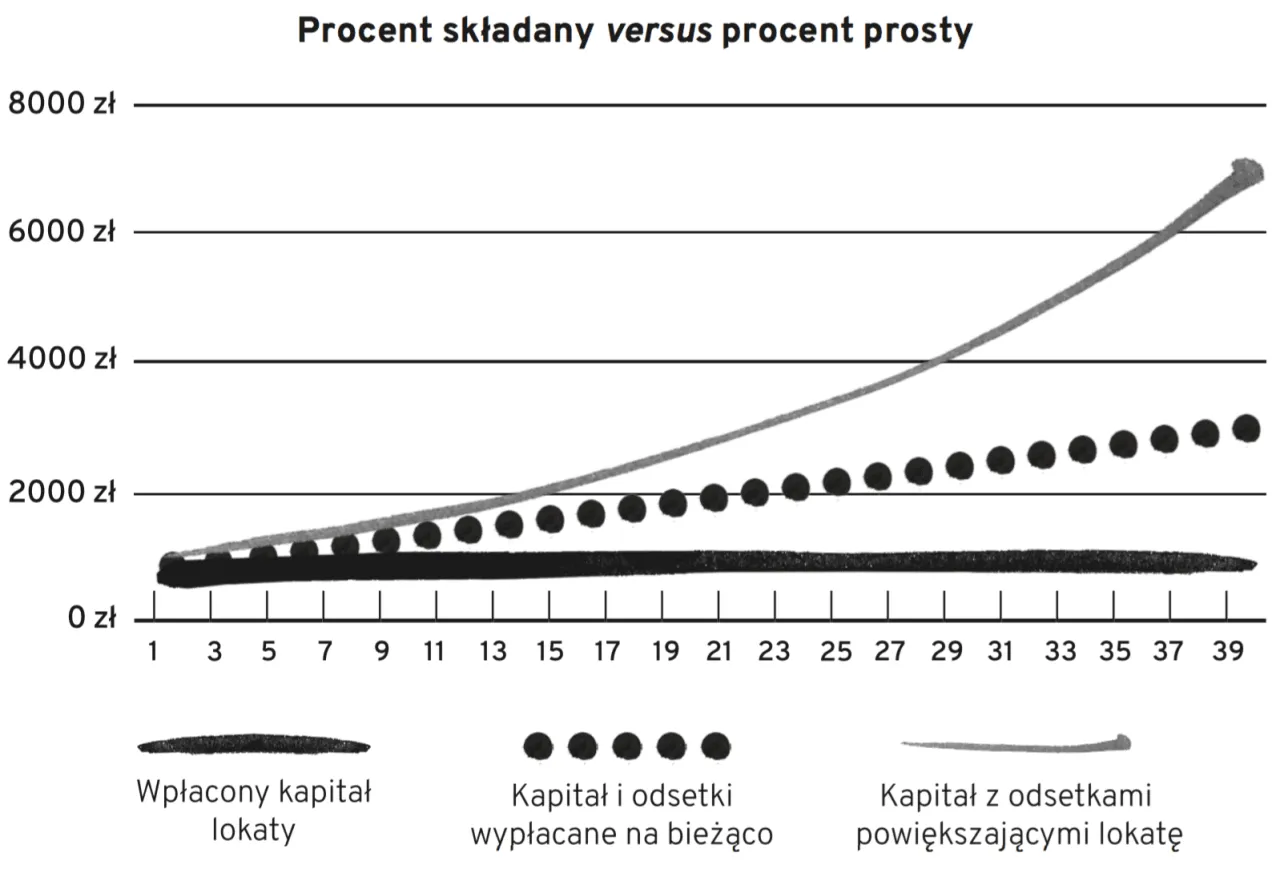
- Rozróżnienie między procentem prostym a składanym jest fundamentalne procent składany generuje wyższe zyski dzięki kapitalizacji odsetek.
- Excel oferuje potężne funkcje finansowe, takie jak FV (Future Value), które znacznie upraszczają obliczenia, zwłaszcza przy procencie składanym.
Zrozum kluczowe pojęcia: oprocentowanie, kapitalizacja i podatek Belki
Zanim zagłębimy się w arkusz kalkulacyjny, musimy upewnić się, że rozumiemy podstawowe mechanizmy rządzące lokatami. W mojej praktyce zauważyłam, że wiele osób pomija te detale, co prowadzi do błędnych wyliczeń.
Oprocentowanie w skali roku to standardowy sposób, w jaki banki prezentują zyskowność lokat. Zawsze jest ono podawane jako stawka roczna, nawet jeśli lokata trwa krócej, na przykład 3 miesiące. Oznacza to, że jeśli masz lokatę na 5% w skali roku, a trwa ona tylko pół roku, faktycznie zarobisz połowę tego oprocentowania, czyli 2,5% od kapitału, zanim uwzględnimy podatek.
Kapitalizacja odsetek to moment, w którym bank dopisuje wypracowane odsetki do Twojego kapitału. Może być roczna, miesięczna, kwartalna, a nawet dzienna. Dlaczego to takie ważne? Bo odsetki dopisane do kapitału zaczynają same generować zysk to właśnie esencja procentu składanego. Im częstsza kapitalizacja, tym szybciej Twoje odsetki zaczynają "pracować" na siebie, co w efekcie prowadzi do wyższego zysku końcowego. Z mojego doświadczenia wynika, że to właśnie ten element jest najczęściej niedoceniany.
Podatek od zysków kapitałowych (podatek Belki) to stała bolączka każdego oszczędzającego w Polsce. Wynosi on 19% i jest pobierany od wypracowanych odsetek brutto. Co ważne, banki robią to za Ciebie automatycznie Ty otrzymujesz już kwotę netto. Jednak aby świadomie ocenić atrakcyjność lokaty, musisz wiedzieć, ile faktycznie "zabrał" Ci fiskus. Pamiętaj, że podatek ten dotyczy tylko zysku, nie całego kapitału.
Zalety własnego kalkulatora: elastyczność i pełna kontrola nad obliczeniami
Posiadanie własnego kalkulatora lokat w Excelu to coś więcej niż tylko narzędzie to Twoja osobista przewaga. Dlaczego warto poświęcić chwilę na jego stworzenie?
- Pełna elastyczność: Możesz błyskawicznie zmieniać dowolne parametry kwotę lokaty, oprocentowanie, czas trwania czy częstotliwość kapitalizacji i natychmiast zobaczyć, jak wpływają one na Twój zysk.
- Symulacja scenariuszy: Z łatwością porównasz oferty różnych banków, wprowadzając ich dane i sprawdzając, która opcja jest dla Ciebie najkorzystniejsza. To pozwala na podejmowanie świadomych decyzji.
- Kontrola i przejrzystość: Widzisz dokładnie, jak działają obliczenia, co buduje Twoje zaufanie do wyników. Nie musisz polegać na gotowych kalkulatorach online, których mechanizmów nie znasz.
- Edukacja finansowa: Tworzenie własnego kalkulatora to świetna lekcja z zakresu finansów osobistych i działania procentu składanego.
Obliczanie zysku z lokaty krok po kroku: metoda dla początkujących
Zacznijmy od najprostszych obliczeń, które są fundamentem dla bardziej zaawansowanych. Upewnij się, że masz otwarty pusty arkusz Excela.
Krok 1: Przygotuj swój arkusz jakie dane będą Ci potrzebne?
Pierwszym krokiem jest zorganizowanie danych wejściowych. W mojej opinii, kluczem do czytelnego i funkcjonalnego kalkulatora jest umieszczenie każdej zmiennej w osobnej komórce. To ułatwia późniejsze modyfikacje i analizę.
Wprowadź następujące dane do swojego arkusza, każdą w osobnej komórce (np. w kolumnie A, z opisem w kolumnie B):
- Kwota lokaty: np. 10000 (zł)
- Oprocentowanie nominalne w skali roku: np. 5% (wpisz jako 0,05 lub 5% bezpośrednio w komórce)
- Czas trwania lokaty: np. 3 (miesiące)
- Częstotliwość kapitalizacji odsetek: np. na koniec okresu (dla uproszczenia na początek)
Krok 2: Prosta formuła na zysk brutto (przed opodatkowaniem)
Dla lokat z jednorazową kapitalizacją na koniec okresu (czyli z procentem prostym) formuła jest stosunkowo prosta. Musimy jednak pamiętać o proporcjonalnym dostosowaniu oprocentowania rocznego do faktycznego czasu trwania lokaty. Jeśli lokata trwa krócej niż rok, dzielimy oprocentowanie roczne przez odpowiednią liczbę okresów w roku.
Przyjmijmy, że:
- Kwota lokaty znajduje się w komórce
B1 - Oprocentowanie roczne w komórce
B2 - Czas trwania lokaty w miesiącach w komórce
B3
Formuła na zysk brutto (odsetki przed opodatkowaniem) będzie wyglądać następująco:
=B1*B2*(B3/12)
W tym przykładzie B3/12 przelicza liczbę miesięcy na ułamek roku. Jeśli lokata trwałaby np. 6 miesięcy, byłoby to 6/12, czyli 0,5 roku.
Krok 3: Jak prawidłowo uwzględnić podatek Belki (19%) w formule?
Jak już wspomniałam, podatek Belki wynosi 19% i jest pobierany od wypracowanych odsetek brutto. Aby uzyskać zysk netto, musimy odjąć ten podatek od kwoty brutto. Możemy to zrobić, mnożąc zysk brutto przez (1-0,19), czyli przez 0,81. To jest kwota, która faktycznie zostanie na Twoim koncie.
Modyfikując poprzednią formułę, aby uwzględnić podatek Belki, otrzymujemy:
=B1*B2*(B3/12)*(1-0.19)
Ta formuła od razu poda Ci zysk netto, czyli to, co realnie zarobisz.
Praktyczny przykład: Obliczamy zysk netto z lokaty 3-miesięcznej
Przejdźmy do konkretów. Wyobraź sobie, że wpłacasz 10 000 zł na lokatę 3-miesięczną z oprocentowaniem 5% w skali roku. Kapitalizacja następuje na koniec okresu. Zobaczmy, ile faktycznie zarobisz.
Wprowadź dane do Excela:
| Komórka | Wartość | Opis |
|---|---|---|
| B1 | 10000 | Kwota lokaty |
| B2 | 0.05 | Oprocentowanie roczne (5%) |
| B3 | 3 | Czas trwania lokaty (miesiące) |
Następnie w dowolnej wolnej komórce (np. B5) wpisz formułę na zysk netto:
=B1*B2*(B3/12)*(1-0.19)
Oczekiwany wynik to około 101,25 zł. To jest Twój realny zysk netto po trzech miesiącach.
Procent składany w Excelu: jak obliczyć zysk przy częstej kapitalizacji?
Teraz przejdziemy do bardziej zaawansowanych, ale niezwykle ważnych obliczeń, które pozwolą Ci w pełni wykorzystać potencjał Excela czyli do procentu składanego.
Czym jest procent składany i dlaczego zwiększa Twój zysk?
Procent składany to prawdziwy "ósmy cud świata", jak mawiał Einstein. Działa on na zasadzie "odsetki od odsetek". Oznacza to, że po każdym okresie kapitalizacji (np. miesiącu), wypracowane odsetki są dopisywane do Twojego kapitału początkowego. W kolejnym okresie odsetki naliczane są już od powiększonej kwoty. W przeciwieństwie do procentu prostego, gdzie odsetki są naliczane zawsze od tej samej kwoty początkowej, procent składany generuje wykładniczy wzrost kapitału. Im częstsza kapitalizacja (miesięczna, dzienna), tym szybciej Twój kapitał rośnie, a Ty zarabiasz więcej.
Uniwersalna formuła na zysk z lokaty z kapitalizacją miesięczną i kwartalną
Ogólny wzór na procent składany wygląda następująco:
Kapitał końcowy = Kapitał początkowy * (1 + oprocentowanie / liczba kapitalizacji w roku)^(liczba kapitalizacji w roku * liczba lat)
Przełóżmy to na Excela. Załóżmy, że:
- Kwota lokaty:
B1 - Oprocentowanie roczne:
B2 - Czas trwania lokaty w latach:
B3(jeśli w miesiącach, toB3/12) - Liczba kapitalizacji w roku:
B4(np. 12 dla miesięcznej, 4 dla kwartalnej, 1 dla rocznej)
Formuła na kapitał końcowy brutto będzie wyglądać tak:
=B1*(1+(B2/B4))^(B4*B3)
Aby obliczyć zysk netto, musimy odjąć kapitał początkowy od kapitału końcowego brutto, a następnie zastosować podatek Belki:
=(B1*(1+(B2/B4))^(B4*B3)-B1)*(1-0.19)
Pamiętaj, aby B3 było wyrażone w latach. Jeśli masz czas trwania w miesiącach (np. w komórce C3), użyj (C3/12) zamiast B3.
Błąd, którego musisz unikać: Dzielenie oprocentowania i mnożenie okresów
To jeden z najczęstszych błędów, jakie widzę w arkuszach moich klientów. Kiedy stosujesz wzór na procent składany, kluczowe jest, aby zarówno stopa procentowa, jak i liczba okresów w potędze odnosiły się do *tego samego okresu kapitalizacji*. Jeśli kapitalizacja jest miesięczna, musisz podzielić oprocentowanie roczne przez 12 (aby uzyskać oprocentowanie miesięczne) i pomnożyć liczbę lat przez 12 (aby uzyskać całkowitą liczbę miesięcy). Nie wolno zapominać o żadnym z tych kroków, bo wynik będzie błędny.
Przykład porównawczy: Lokata roczna z kapitalizacją roczną vs. miesięczną
Zobaczmy, jak częstotliwość kapitalizacji wpływa na zysk. Załóżmy lokatę:
- Kwota: 10 000 zł
- Oprocentowanie: 5% w skali roku
- Czas trwania: 1 rok
Scenariusz 1: Kapitalizacja roczna
Dane w Excelu:
| Komórka | Wartość | Opis |
|---|---|---|
| B1 | 10000 | Kwota lokaty |
| B2 | 0.05 | Oprocentowanie roczne |
| B3 | 1 | Czas trwania (lata) |
| B4 | 1 | Kapitalizacja w roku (roczna) |
Formuła na zysk netto:
=(B1*(1+(B2/B4))^(B4*B3)-B1)*(1-0.19)
Wynik: 405 zł
Scenariusz 2: Kapitalizacja miesięczna
Dane w Excelu:
| Komórka | Wartość | Opis |
|---|---|---|
| C1 | 10000 | Kwota lokaty |
| C2 | 0.05 | Oprocentowanie roczne |
| C3 | 1 | Czas trwania (lata) |
| C4 | 12 | Kapitalizacja w roku (miesięczna) |
Formuła na zysk netto:
=(C1*(1+(C2/C4))^(C4*C3)-C1)*(1-0.19)
Wynik: 415,86 zł
Jak widzisz, różnica wynosi ponad 10 zł na korzyść kapitalizacji miesięcznej. Przy większych kwotach i dłuższych okresach ta różnica będzie znacznie większa. To pokazuje, jak ważne jest uwzględnienie częstotliwości kapitalizacji.
Poznaj moc funkcji finansowych Excela: sposób dla zaawansowanych
Jeśli chcesz pójść o krok dalej i jeszcze bardziej uprościć swoje obliczenia, Excel oferuje wbudowane funkcje finansowe. Moją ulubioną w kontekście lokat jest funkcja FV.
Czym jest funkcja FV (Future Value) i jak upraszcza obliczenia?
FunkcjaFV (z ang. Future Value, czyli wartość przyszła) to potężne narzędzie w Excelu, które automatycznie oblicza przyszłą wartość inwestycji, w tym lokat bankowych. Jest szczególnie przydatna przy procencie składanym, ponieważ sama zajmuje się złożonymi obliczeniami potęgowania, eliminując potrzebę ręcznego tworzenia długich i podatnych na błędy formuł. Dzięki niej możesz szybko i precyzyjnie dowiedzieć się, ile wyniesie Twój kapitał na koniec okresu inwestycji.
Składnia funkcji FV: Jak poprawnie wprowadzić argumenty (stopa, liczba_okresów, wb)?
Składnia funkcji FV wygląda następująco:
FV(stopa; liczba_okresów; rata; [wb]; [typ])
Dla prostych lokat jednorazowych kluczowe argumenty to:
-
stopa: To oprocentowanie na okres kapitalizacji. Jeśli oprocentowanie roczne wynosi 5%, a kapitalizacja jest miesięczna, tostopabędzie5%/12. -
liczba_okresów: To całkowita liczba okresów kapitalizacji w całym czasie trwania lokaty. Jeśli lokata trwa 1 rok, a kapitalizacja jest miesięczna, toliczba_okresówbędzie1*12, czyli 12. -
rata: Ten argument jest używany dla regularnych wpłat (np. co miesiąc). Dla lokaty jednorazowej pozostawiamy go pusty lub wpisujemy0. -
[wb](wartość bieżąca): To początkowy kapitał, czyli kwota, którą wpłacasz na lokatę. Zawsze wprowadza się ją z minusem, ponieważ dla Excela jest to "wypływ" gotówki z Twojej kieszeni. -
[typ]: Określa, czy płatności są dokonywane na początku (1) czy na końcu (0) okresu. Dla lokat zazwyczaj pozostawiamy pusty lub wpisujemy0.
Praktyczne zastosowanie FV: Błyskawiczne obliczenie wartości lokaty na koniec okresu
Wykorzystajmy funkcję FV do obliczenia przyszłej wartości lokaty z kapitalizacją miesięczną. Załóżmy, że:
- Kwota lokaty (
wb): 10 000 zł (w komórceB1) - Oprocentowanie roczne: 5% (w komórce
B2) - Czas trwania lokaty: 1 rok (w komórce
B3) - Kapitalizacja: miesięczna (12 razy w roku, w komórce
B4)
Formuła w Excelu będzie wyglądać tak:
=FV(B2/B4; B3*B4; 0; -B1)
Wynik tej funkcji to około -10511,62 zł. Znak minus oznacza, że jest to kwota, którą "otrzymujesz" z powrotem. Wartość bezwzględna (10511,62 zł) to kapitał końcowy brutto.
Jak z wyniku funkcji FV obliczyć czysty zysk netto?
Funkcja FV zwraca nam kapitał końcowy brutto (kapitał początkowy + odsetki brutto). Aby uzyskać czysty zysk netto, musimy wykonać kilka dodatkowych kroków, które są identyczne jak w przypadku ręcznych obliczeń:
-
Oblicz zysk brutto: Od wyniku
FV(bez znaku minus) odejmij kapitał początkowy. - Oblicz podatek Belki: Pomnóż zysk brutto przez 19% (0,19).
- Oblicz zysk netto: Od zysku brutto odejmij kwotę podatku Belki.
Kontynuując nasz przykład:
- Wynik
FV(kapitał końcowy brutto): 10511,62 zł - Kapitał początkowy (
B1): 10000 zł
W Excelu możesz to zrobić w kilku komórkach lub w jednej złożonej formule:
- W komórce
C1(Kapitał końcowy brutto):=ABS(FV(B2/B4; B3*B4; 0; -B1))(użycieABSusuwa znak minus) - W komórce
C2(Zysk brutto):=C1-B1 - W komórce
C3(Podatek Belki):=C2*0.19 - W komórce
C4(Zysk netto):=C2-C3
Alternatywnie, cała formuła na zysk netto:
=(ABS(FV(B2/B4; B3*B4; 0; -B1))-B1)*(1-0.19)
Wynik: 415,86 zł. Jak widać, jest to ten sam wynik, co w poprzednim przykładzie, ale uzyskany za pomocą wbudowanej funkcji Excela.

Twój własny, uniwersalny kalkulator lokat w Excelu: zbuduj go w 5 minut
Teraz, gdy znasz już wszystkie kluczowe elementy, połączmy je w jeden, uniwersalny kalkulator. Moim celem jest, abyś mógł go zbudować szybko i intuicyjnie.
Projektujemy interfejs: Pola do wpisania kwoty, oprocentowania, okresu i kapitalizacji
Zacznij od stworzenia prostego i czytelnego interfejsu w swoim arkuszu. To podstawa dobrego kalkulatora. Proponuję następujący układ:
- Komórka B1: Kwota lokaty (np. 10000)
- Komórka B2: Oprocentowanie roczne (np. 0.05 lub 5%)
- Komórka B3: Czas trwania lokaty (np. 12 dla 12 miesięcy, 1 dla 1 roku zdecyduj, czy wolisz miesiące czy lata i bądź konsekwentny)
- Komórka B4: Jednostka czasu (np. "miesiące" lub "lata" to tylko etykieta, ale pomaga w zrozumieniu)
- Komórka B5: Częstotliwość kapitalizacji (tutaj możesz użyć listy rozwijanej z opcjami: "roczna", "kwartalna", "miesięczna", "dzienna" to znacznie ułatwi obsługę. Listę rozwijaną tworzy się w zakładce "Dane" -> "Poprawność danych" -> "Lista").
Wdrażamy inteligentną formułę z funkcją "JEŻELI" do obsługi różnych okresów kapitalizacji
To jest serce Twojego uniwersalnego kalkulatora. Użyjemy funkcji JEŻELI (IF) w połączeniu z FV, aby kalkulator automatycznie dostosowywał obliczenia do wybranej częstotliwości kapitalizacji. Będziemy musieli określić liczbę kapitalizacji w roku na podstawie wyboru użytkownika.
Załóżmy, że w komórce B5 masz wybraną częstotliwość kapitalizacji ("roczna", "kwartalna", "miesięczna", "dzienna"). Stwórzmy pomocniczą komórkę (np. B6), która przeliczy to na liczbę kapitalizacji w roku:
=JEŻELI(B5="roczna";1;JEŻELI(B5="kwartalna";4;JEŻELI(B5="miesięczna";12;JEŻELI(B5="dzienna";365;1))))
Teraz, mając liczbę kapitalizacji w roku (w B6), możemy zbudować formułę na kapitał końcowy brutto, uwzględniając, że czas trwania (B3) jest w miesiącach:
=ABS(FV(B2/B6; (B3/12)*B6; 0; -B1))
Jeśli B3 jest w latach, formuła będzie prostsza: =ABS(FV(B2/B6; B3*B6; 0; -B1)). Zawsze upewnij się, że liczba_okresów w FV jest całkowitą liczbą okresów kapitalizacji w całym czasie trwania lokaty.
Finalne obliczenia: Automatyczne wyświetlanie zysku brutto, kwoty podatku i zysku netto
Teraz, gdy masz już kapitał końcowy brutto (np. w komórce C1, gdzie umieściłeś formułę z poprzedniego kroku), możesz łatwo wyświetlić wszystkie kluczowe wyniki:
-
Komórka D1 (Zysk brutto):
=C1-B1(Kapitał końcowy brutto minus kapitał początkowy) -
Komórka D2 (Kwota podatku Belki):
=D1*0.19(19% z zysku brutto) -
Komórka D3 (Zysk netto):
=D1-D2(Zysk brutto minus podatek)
Twój uniwersalny kalkulator jest gotowy! Teraz możesz zmieniać dane wejściowe i obserwować, jak zmieniają się wyniki, co pozwoli Ci podejmować lepsze decyzje finansowe.
Co jeszcze warto wiedzieć? Najczęstsze pytania i pułapki
W mojej pracy często spotykam się z dodatkowymi pytaniami i wątpliwościami dotyczącymi obliczeń lokat. Oto kilka z nich, które mogą okazać się pomocne.
Czy liczba dni w miesiącu (30 vs 31) ma znaczenie w obliczeniach?
W praktyce bankowej, zwłaszcza przy kapitalizacji dziennej, banki mogą stosować różne konwencje dotyczące liczby dni w roku (np. 360, 365, 366 dni). Może to prowadzić do minimalnych różnic w naliczanych odsetkach. Jednak dla większości osobistych obliczeń i symulacji, przyjęcie 365 dni w roku (lub 366 w przestępnym) jest wystarczająco precyzyjne i znacznie upraszcza formuły. Różnice są zazwyczaj na tyle małe, że nie mają znaczącego wpływu na Twoje decyzje.
Jak dostosować formułę, jeśli lokata jest wyrażona w dniach, a nie miesiącach?
Jeśli czas trwania lokaty jest podany w dniach (np. 90 dni), musisz odpowiednio dostosować zarówno oprocentowanie, jak i liczbę okresów. Oprocentowanie roczne (np. B2) należy przeliczyć na dzienne, dzieląc je przez 365 (lub 366). Liczba dni trwania lokaty (np. w komórce B3) będzie wtedy bezpośrednio liczbą okresów.
Przykład dla funkcji FV, jeśli B3 to liczba dni, a kapitalizacja jest dzienna (B6=365):
=ABS(FV(B2/B6; B3; 0; -B1))
Jeśli kapitalizacja jest inna niż dzienna, ale lokata jest w dniach, musisz przeliczyć dni na ułamek roku/miesiąca/kwartału, np. B3/365 jako liczbę lat.
Przeczytaj również: mBank wpłatomat: Limity, opłaty, awarie wszystko, co musisz wiedzieć
Obliczenia dla lokat progresywnych czy to możliwe w prostym arkuszu?
Lokaty progresywne, gdzie oprocentowanie zmienia się w zależności od okresu (np. wyższe oprocentowanie w drugim półroczu), są znacznie bardziej skomplikowane do obliczenia w prostym arkuszu. Wymagają one rozbicia lokaty na poszczególne etapy, z których każdy ma inne oprocentowanie i czas trwania. Następnie kapitał końcowy z jednego etapu staje się kapitałem początkowym dla kolejnego. Jest to możliwe do wykonania w Excelu, ale wykracza poza zakres prostego kalkulatora i wymaga bardziej zaawansowanych formuł lub nawet VBA. Na początek skup się na standardowych lokatach, a do progresywnych wrócisz, gdy poczujesz się pewniej z Excelem.

